Koordinatensystem

Ein Koordinatensystem dient zur eindeutigen Zuweisung von Punkten in dimensionalen Räumen. Die im Alltag und auch dem größten Teil der wissenschaftlichen Arbeit am weitesten verbreiteten Systeme bilden sich auf 1,2- oder 3-Achsen ab. Man spricht in diesem Zusammenhang auch von Dimensionen. So sind vor allem die Abkürzungen dessen, 1D, 2D und 3D, sehr geläufig. Grundsätzlich sind Koordinatensysteme ein Teilgebiet der Mathematik.

1-Dimensional

Ein einachsiges Koordinatensystem ist nicht für viele Fälle geeignet. Da sich der Raum nur in eine Dimension erstreckt können nur Punkte entlang der Achse beschrieben werden. Ein Beispiel für ein eindimensionales Koordinatensystem wäre ein Zahlenstrahl mit reellen Zahlen.

2-Dimensional

Die Darstellung von Koordinaten auf 2 Achsen kann man sich auch vorstellen aus Darstellung auf einer Fläche. Die 2 Achsen spannen eine Ebene auf, auf der jeder beliebige Punkt eindeutig zu bestimmen ist. Die Beschreibung der Punkt kann auf unterschiedliche Arten erfolgen:

Kartesische Koordinaten

Darstellung der Koordinate P(7,4)

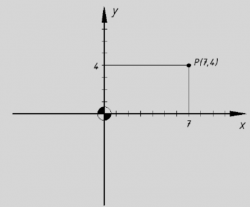
Die verbreitetste Form die Koordinaten darzustellen sind über kartesische Koordinaten. Die Koordinate besteht dabei aus genau 2 Elementen: der Wert der X und der Y-Komponente. Die einheitliche Darstellung sieht dann wie folgt aus: (X,Y). Ein Beispiel wäre (148,537). Dabei können der X und der Y-Wert jeden beliebigen Wert einer reellen Zahl annehmen und beschreiben dabei die Entfernung zum Nullpunkt. Wichtig sind hierbei die Vorzeichenkonventionen, da die Entfernung in diesem Fall nicht gleich der Betrag ist. Die mathematische Notation ist

-Kartesische Koordinate:= {(X,Y)|y=a*x, mit X,Y ∈ R (das R für reelle Zahlen wird üblicherweise mit zwei Strichen dargestellt).

Das Koordinatensystem selbst besteht dabei aus 2 Achsen, die tangential (rechtwinklig) aufeinander stehen. Durch das angeben von mehreren Punkten oder Vektoren können in diesem System Geraden, Kurven oder Flächen dargestellt werden.

Verschiebbare Koordinaten

Verschiebbare Koordinaten funktionieren im Grunde wie kartesische Koordinaten. Der Unterschied liegt darin, dass sich bei verschiebbaren Koordinaten der Ursprung (0,0) verschieben lässt. Damit verschieben sich proportional alles restlichen Koordinaten. Der Ursprung lässt sich hierbei um einen Bestimmten X und Y-Wert verschieben, sowie um einen Winkel α drehen. Man nennt dies eine Hauptachsenverschiebung. Um Fehler zu vermeiden sollte hier in Schritten gearbeitet werden.

• Beispiel: Koordinate = (12,14); das Koordinatensystem soll um (4,5) und α=45° verschoben werden

1. x_neu* = x_alt - x_verschiebung = 12 - 4 = 8
2. y_neu* = y_alt - y_verschiebung = 14 - 5 = 9
3. cos(45°) = sin(45°) = 1/Wurzel[2]
4. Neue Koordinaten = (8/Wurzel[2],9/Wurzel[2])

Relative Koordinaten

Relative Koordinaten sind kartesische Koordinaten mit Bezug auf eine bereits angegebene Koordinate. In CAD-Programmen werden diese meist mit einem @ eingegeben.

• Beispiel: Die Koordinatenpaare A(5,8) und B(2,12), sowie A(5,8) und A(@-3,4) beschreiben in beiden Fällen die gleichen beiden Punkte.

Polarkoordinaten

Polarkoordinaten werden zur Darstellung komplexer Zahlen verwendet. Eine Komplexe z = x + i*y kann auch als Polarkoordinate mit z = r*(cox(a) + sin(a)*i) darstellen. Dabei ist r ein Radius, der sich aus der Wurzel von x²+y² ergibt (Satz des Pythagoras) und der Winkel a aus den trigonometrischen Funktionen. Damit liegt der Punkt z genau in der Schnittstelle des Radius auf dem Winkel a vom Urspung. Wird der Winkel im Bogenmaß angegeben, wie in der Mathematik, darf dieser nur in den Grenzen 0 und 2*pi liegen. Liegt er darüber oder darunter wird der Wert 2*pi (entspricht 260° und ändert den Winkel somit nicht) so lange subtrahiert beziehungsweise addiert, bis er dazwischen liegt. In CAD-Programmen wird der Winkel hingegen oft im Radiant, also in °, angegeben.

3-Dimensional

Für den 3-dimensionalen Raum verwendet man meist ein kartesisches Koordinatensystem mit drei Achsen. Die X-, Y- und Z-Achse stehen dabei alle rechtwinklig zueinander. Durch die Angabe der drei Bewegungsrichtungen lassen sich alle Punkte eines Raumes erfassen. Ebenfalls können mit Vektoren Geraden, Flächen und Volumenkörper beschrieben werden. Die Beschreibung von Volumenkörpern gestaltet sich allerdings als mathematisch sehr komplex und findet daher in alltäglichen Anwendungen, selbst bei Ingenieuren, kaum Verwendung.

Literatur und Quellen

• Einstieg in CAD; Harald Vogel; 2004; Verlag: Carl Hanser Verlag GmbH & Co. KG; ISBN: 978-3-446-22381-3
• Mathematisches Wörterbuch. von Leopold Natan